Theory of the Minimum Spanning Tree Problem [Part 1]

a connected graph with its minimum spanning tree

This example was taken from taken from Wikipedia

In this blog post, I will discuss the inner structure and some theoretical results behind the minimum spanning tree problem in the context of undirected graphs. Firstly, we define a spanning subgraph and a minimum spanning subgraph. After proving some results regarding the structure of the minimum spanning tree problem, we develop two famous algorithms - Prim’s algorithm and Kruskal’s algorithm using the inner structure of the problem discussed in results proved before. The point of this approach which firstly develops the theory and then develops the algorithm is to shed some light on the key ideas behind those algorithms. After having discussed the structure of this problem, both algorithms seem completely natural and their correctness suddenly becomes evident. This is particularly important since both of these algorithms belong to the category of greedy algorithms, which gradually build the optimal solution to the original problem by making only the locally optimal choices. Clearly, it is common that the correctness proof of such algorithms becomes quite involved.

Definition 1: a spanning subset and a spanning tree

Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Then a subgraph $G' = (V,A)$ where $A \subseteq E$ is a spanning subgraph of the graph G if the graph $G'=(V, A)$ is connected. If $G'$ is a tree, we say $G'$ is a spanning tree of the graph G.

Now, we state and prove two important theorems which guarantee existence of minimum spanning tree for every connected graph.

Theorem 1: Every connected graph has a spanning tree.

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Then $G$ has a spanning tree and hence a spanning subgraph.

Proof: We will prove by induction on the number of vertices $|V|$.
Basis: Suppose $|V|$ = 1. Trivially, $G$ is connected. The graph $(V, \emptyset)$ is trivially a spanning tree. This establishes the basis.
Induction Hypothesis: Suppose that for all graphs $G=(V,E)$, with $|V| = n - 1$, the claim holds.
Induction Step: Now consider an undirected connected graph $G=(V, E)$ with the vertex set $V$ such that $|V| = n, n > 1$. Since $|V| \ge 1$, let $u \in V$. Since the graph $G$ is connected, $\forall v \in V$, there exists a path $v \rightsquigarrow u$. Now, by the previous statement, there exists an edge $(v, u)$ for some $v \in V, v \neq u$. Consider the subgraph $G' = (V', E')$ where: $V' = V - \{ u \}$
$E' = E - \{ (v, u) | (v, u) \in E \}$
Observe that $G'$ is a subgraph of $G$. Since $G$ was connected, so is $G'$ because otherwise $G$ cannot be connected. By Induction Hypothesis, $G'$ has a spanning tree, say $T = (V', A)$ for some $A \subseteq E$. Now consider $T' = (V, A')$ where $A' = A \cup \{ (v, u) \}$. We claim that $T'$ is a spanning tree of the graph $G$. Since $u \not \in V'$, $A'$ does not induce a cycle in $T'$ and connects $V$. Since $T$ was a tree which is a subgraph of $G$, all vertices in $V'$ are also connected in $T$ and the edge $(u,v)$ connected $u$ to all of vertices in $V'$. Therefore, since $T'$ is a connected graph without cycles, we deduce it is a tree. Since vertices of $T'$ are $V$, $T'$ is a spanning tree of $G$.
This completes the proof. $\blacksquare$

Remark: Does every undirected graph have a spanning tree? The answer is no, because any graph without edges and more than one vertex does not have a spanning tree. Therefore, the connectedness assumption of the graph is a crucial assumption which cannot be dropped.

Definition 2: a minimum spanning subset and a minimum spanning tree

Let $w : E \to \mathbb{R}$ be a positive edge cost function. Define $w(A)= \sum_{(u,v) \in A} w((u, v))$. We say that a spanning subset $A \subseteq E$ of $G$ is minimal if $w(A)$ is minimal amongst all possible spanning subgraphs of $G$.

Corollary 1: Every connected graph has a minimum spanning tree.

Proof: By Theorem 1, every connected graph has a spanning tree. Since the number of spanning trees of any connected graph is finite, we deduce that for every connected graph there exists at least one minimum spanning tree. $\blacksquare$

Theorem 2: Assuming the strictly positive edge cost function, every minimal spanning subgraph is a tree.

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Let $w : E \to \mathbb{R}$ be a positive edge cost function. Then every minimal spanning subgraph of G is a tree.

Proof: (By contradiction)

Let $(V,A), A \subseteq E$ be a minimal spanning subgraph of the graph $G$. Assume, for the sake of contradiction, that $(V,A)$ is not a tree. By definition of $A$, $(V,A)$ is connected. Since $(V,A)$ is connected and it is not a tree, it must be the case $A$ has a cycle. Suppose $v_1, v_2, \ldots v_k = v_1$ is a cycle in the graph $(V, A)$. Now select any edge $(v_i, v_j), 1 \leq i, j \leq k$. Consider $A' = A - \{ (v_i, v_j) \}$ and the graph $G'=(V, A')$. Since $v_1, v_2, \ldots v_k = v_1$ is a cycle, vertices $(v_i, v_j), 1 \leq i, j \leq k$ still remain connected in $G'$ along some path $v_i \rightsquigarrow v_{i+1} \ldots \rightsquigarrow v_j$ in $G$. Moreover, we claim that $G'$ is connected. Select $(u, v) \in V \times V$. Since $A$ is a spanning subset of $G$, there exists a path $u \rightsquigarrow v \subseteq E$. We split in cases depending on whether $(v_i, v_j) \in u \rightsquigarrow v$.

Suppose $(v_i, v_j) \not \in u \rightsquigarrow v$. Then $u$ and $v$ remain connected in $G'$ by existence of the path $u \rightsquigarrow v$ in $G$. By construction of $G'$, $u \rightsquigarrow v$ is in $G'$.

Suppose $(v_i, v_j) \in u \rightsquigarrow v$. Then $u$ and $v$ remain connected in $G'$ by existence of the path $u \rightsquigarrow v_i \rightsquigarrow v_{i+1} \ldots \rightsquigarrow v_j \rightsquigarrow v$ in $G$. By construction of $G'$, $u \rightsquigarrow v_i \rightsquigarrow v_{i+1} \ldots \rightsquigarrow v_j \rightsquigarrow v$ is in $G'$.

Since $(u, v)$ was arbitrary, we deduce $G'$ is connected so $G'$ must be a spanning subgraph of $G$. Observe that $w(A') = w(A) - w((v_i, v_j))$. Since $w$ is a positive edge cost function, $w((v_i, v_j)) > 0$ so $w(A') < w(A)$. This contradicts the minimality of $A$. The assumption $(V,A)$ is not a tree was wrong. Hence $(V,A)$ must be a a tree. This completes the proof. $\blacksquare$

Definitions stated above ensure the (minimum) spanning trees or subgraphs are precisely defined while above proved theorems guarantee the existence of spanning tree in connected graphs. Although these results may be basic, they outline a general setup for more interesting results, such as the following one.

Theorem 3: Uniqueness of a minimum spanning tree

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Let $w : E \to \mathbb{R}$ be an injective edge cost function. Then the minimum spanning tree of the graph $G$ must be unique.

Proof: (By contradiction)

Suppose, for the sake of contradiction, that there exist two distinct minimum spanning trees $T=(V,A)$ and $T'=(V, A')$. Since $T$ and $T'$ are distinct, let $(u,v)$ be the minimum cost edge that is not present in both $A$ and $A'$. By the fact $w$ is injective, the edge $(u,v)$ is the unique edge that is not present in both $A$ and $A'$ of the minimum cost. Assume, without loss of generality, that $(u,v)$ is present in $A$ and hence not present in $A'$. Since $T'$ is a spanning tree, there exists the unique path $u \rightsquigarrow v$. We claim there exists an edge $(x, y)$ such that $(x,y) \in u \rightsquigarrow v$ where $u \rightsquigarrow v$ is a path in $T'$ and $(x, y) \not \in A$.
By construction of $(u,v)$, the path $u \rightsquigarrow v \in T'$ can be decomposed as $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ where $y$ is possibly $v$ and $u \neq x$. If the path $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ is entirely included in $T$, we obtain a cycle $u \rightsquigarrow x \rightarrow y \rightsquigarrow v \rightarrow u$ which contradicts the fact $T$ was a tree. Hence it must be the case there exists $(x, y) \in A'$ such that $(x,y) \in u \rightsquigarrow v$ where $u \rightsquigarrow v$ is a path in $T'$ and $(x, y) \not \in A$. Observe that $w((x,y)) > w((u,v))$.
Now consider the graph $T''=(V, A'')$ where $A'' = (A' - \{ (x,y) \}) \cup \{(u,v)\}$. We claim that $T''$ is as spanning tree of $G$. By the fact $u \rightsquigarrow v$ is the unique path from $u$ to $v$ in the tree $T'$, the graph $(V,(A' - \{ (x,y) \}))$ is split into two disjoint connected components, one containing $u$ and the other one containing $v$, say $T_u$ and $T_v$ respectively. Observe that $T_u$ and $T_v$ are actually subtrees of $T'$. Since $u,v$ reside in disjoint connected components of $(V,(A' - \{ (x,y) \}))$, $T_u$ and $T_v$, addition of an edge $(u,v)$ to $(A' - \{ (x,y) \})$ connects $u$ and $v$ without induction of cycle so the graph $T''$ must be connected. Moreover, since $T_u$ and $T_v$ were subtrees and are joined by a single edge $(u,v)$ without cycle, we deduce $T''$ is a tree. Since the vertex set of $T''$ is $V$ and $T''$ is a tree, we deduce $T''$ is spanning so $T''$ is a spanning tree of the graph $G$.
Now consider $w(T'')$.

Since $w(T'') < w(T')$ and $T''$ is a spanning tree, $T'$ cannot be a minimum spanning tree. This is a contradiction. The assumption $G$ has distinct minimum spanning trees was wrong, so we deduce $G$ has the unique minimum spanning tree, as claimed. $\blacksquare$

It turns out that in case of connected graphs, there always exists a minimum spanning tree containing the minimum cost edge.

Theorem 4: There exists a minimum spanning tree containing minimum cost edge.

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Let $w : E \to \mathbb{R}$ be an edge cost function. Let $(u,v)$ be a not necessarily unique edge with the minimum cost $w$ amonst all edges in $E$. Then there exists a minimum spanning tree of the graph $G$ containing $(u,v)$.

Proof: (By contradiction)

Let $T=(V,A)$ be a minimum spanning tree of the graph $G$ which does not include an edge $(u,v)$, that is, $(u,v) \not \in A$. Since $T$ is a tree, there exists an unique path $u \rightsquigarrow v$. Since $(u,v) \not \in A$, we decompose the path above as $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ where $y$ possibly equals $v$ and $x \neq u$. Now consider $T' = (V, A - \{ (x, y)\} \cup \{ (u,v) \})$. We will show that $T'$ is a tree and that is spanning. Since the path $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ is unique path from $u$ to $v$ in $T$, removing an edge $(x,y)$ from $T$ disconnects $T$ into two disjoint components (trees), one containing $u$ and the other one containing $v$. Say $T_u$ and $T_v$ respectively. Now since $u$ and $v$ reside in distinct disjoint components $T_u$, $T_v$, addition of the edge $(u,v)$ connects $T_u$ and $T_v$ into a singe component $T'$, since $(u,v)$ cannot induce a cycle. Since $T_u$ and $T_v$ are subtrees of $T$, connecting them via $(u,v)$ produces a tree $T'$. Since $T'$ is a tree with the vertex set $V$, $T'$ is a spanning tree of the graph $G$. We also have:

Since $T$ is a minimum spanning tree, $w(T) \geq w(T')$. Combining this result with the previous one, we obtain $w(T')=w(T)$. Hence $T'$ is a minimum spanning tree of $G$ containing an edge $(u,v)$ of the minimum cost. This completes the proof. $\blacksquare$.

Theorem 5: Elementary cycle properties of a minimum spanning tree

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Let $w : E \to \mathbb{R}$ be an edge cost function. Suppose $v_1, v_2,\ldots, v_k=v_1$ is a cycle in $G$. The following holds:

1. Suppose an edge $(v_i, v_{i+1}), 1 \leq i < k$ is the edge of the maximum cost in the cycle above. If $(v_i, v_{i+1})$ has strictly larger cost then any other edge in the cycle above, $(v_i, v_{i+1})$ cannot be included in a minimum spanning tree of $G$.
2. Suppose $(v_i, v_{i+1}), 1 \leq i < k$ is the edge of the minimum cost from the cycle above. Then $(v_i, v_{i+1})$ may not be included in some minimum spanning tree of $G$.

Proof of 1: (By contradiction)

Let $T=(V,A)$ be a minimum spanning tree of the graph $G$ which does include an edge $(v_i,v_{i+1})$. Consider the graph $T'=(V, A - \{ (v_i,v_{i+1})\})$. Since $T$ was a tree, removing an edge $(v_i,v_{i+1})$ disconnects $T$ into two disjoint connected components $T_{v_i}$ and $T_{v_{i+1}}$ such that $T_{v_i}$ contains $v_i$ and $T_{v_i+1}$ contains $v_{i+1}$. Now, since $v_1, v_2,\ldots, v_k=v_1$ is a cycle, there exists some edge $(u, v)$ on the cycle $v_1, v_2,\ldots, v_k=v_1$ such that $u \in T_{v_i}$ and $v \in T_{v_{i + 1}}$. By assumption regarding $(v_i,v_{i+1})$, we have $w((u,v))<w((v_i,v_{i+1}))$. Now set $T'' = (V, (A - \{ (v_i,v_{i+1})\}) \cup \{ (u,v)\})$. We claim $T''$ is a spanning tree of $G$. Since $T_{v_i}$ and $T_{v_{i+1}}$ are disjoint, adding an edge $(u,v)$ connects $T_{v_i}$ and $T_{v_{i+1}}$ into a single connected component. Since $T_{v_i}$ and $T_{v_{i+1}}$ were subtrees of $T$, we deduce $T''$ is also a tree. Since it includes all vertices from $V$, we deduce $T''$ is a spanning tree. We also have

Since $T''$ is a spanning tree, we deduce $T$ cannot be a minimum spanning tree. This is a contradiction to the fact $T$ was a minimum spanning tree. The assumption $T$ includes $(v_i, v_{i+1})$ was wrong, so we deduce $T$ cannot contain $(v_i, v_{i+1})$. Since $T$ was arbitrary, no minimum spanning tree of $G$ contains $(v_i, v_{i+1})$. This completes the proof. $\blacksquare$

Counterexample for 2:

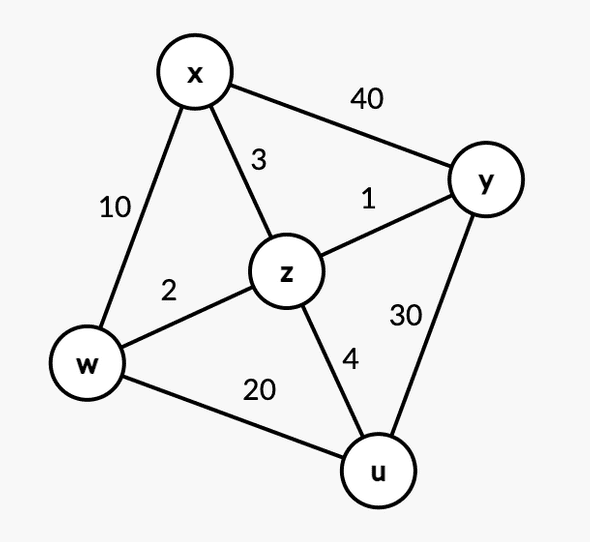
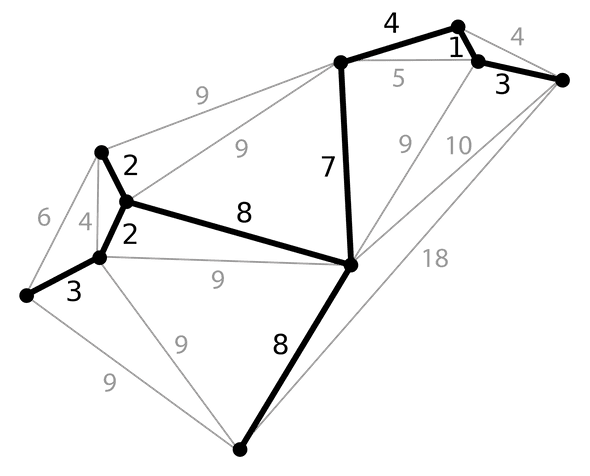
In the graph above, consider the cycle $x,y,u,w,x$. An edge of minimum cost is $(x,w)$. However, the minimum spanning tree of the graph above is:
$T=(\{ x, y, z, u, w\}, \{ (z,x), (z,y), (z,u), (z,w)\})$. Observe that $T$ does not include $(x,w)$.

After having shown the previous results, to prove possibly the most important result regarding the structure of the minimum spanning tree problem, we need to define a concept of the graph cut.

Definition 3: a graph cut, crossing edge

Let $G=(V,E)$ be a graph having the vertex set $V$ and edge set $E$. A cut $(S, V-S)$ is a partition of $V$. An edge $(u,v)$ crosses the cut if $u \in S, v \in (V-S)$.

Now we state and prove the fundamental result regarding the structure of the minimum spanning tree problem. Consider again the Theorem 4. Theorem 4 indicates that it is always ‘safe’ to include a minimum cost edge in a ‘potential’ partial minimum spanning tree, because it must be a part of some minimum spanning tree. However, the step/s after this one are not immediatelly clear and we need a bit more insight into the structure of the minimum spanning tree problem to discover and justify what could be the next possible steps in the process of finding some minimum spanning tree.

Theorem 6: The fundamental cut property of the minimum spanning tree problem

Claim: Let $G=(V,E)$ be an undirected connected graph having the vertex set $V$ and edge set $E$. Let $w : E \to \mathbb{R}$ be an edge cost function. Let $(S, V-S)$ be a cut of the graph $G$. Let $A$ be the set of edges which belong to some minimum spanning tree and assume no edge in $A$ crosses the cut $(S, V-S)$. Let $(u,v)$ be the edge crossing the cut $(S, V-S)$ whose cost $w$ is minimal amongst edges crossing the cut $(S, V-S)$. Then an edge $(u,v)$ belongs to some minimum spanning tree of $G$.

Remark: The intuitive explanation of this claim is the following assertion: Suppose we somehow have a subset of edges $A$ of some minimum spanning tree $T$. If we can find a suitable cut of the graph $(S, V-S)$ and the minimum cost edge $(u,v)$ that crosses the cut, we can safely extend $A$ to $A \cup \{ (u,v) \}$. By ‘safely’ extending we mean that $A \cup \{ (u,v) \}$ is also a subset of some minimum spanning tree. This means that by iteratively finding suitable cuts and minimum weight crossing edges, we eventually construct a minimum spanning tree!

Proof: (By construction)

Let $T=(V,E_T)$ be a minimum spanning tree whose edge set contains $A$, $A \subseteq E_T$. It suffices to show there exists a minimum spanning tree containing edges $A \cup \{ (u,v) \}$. If $(u,v) \in E_T$ then $A \cup \{ (u,v) \} \in E_T$ and the claim holds.
Thus, suppose $(u,v) \not \in E_T$. We will construct a minimum spanning tree containing $(u,v)$. Since $T$ is a spanning tree, there exists the unique path between vertices $u$ and $v$ in $T$. Since $(u,v) \not \in E_T$, and since $u \in S$ and $v \in V - S$ that path decomposes into $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ where $x \in S$, $y \in V - S$ and possibly $x = u$ or $y = v$ but not both $x = u$ and $y = v$. Consider $T' = (V, (E_T - \{ (x,y)\}) \cup \{ (u,v) \})$. We will show $T'$ is a tree which is also a spanning tree such that $A \subseteq E_T - \{ (x,y)\}$.
We will firstly show that $T'$ is indeed a tree. Since $T$ is a tree, the path $u \rightsquigarrow x \rightarrow y \rightsquigarrow v$ is unique so $E_T - \{ (x,y)\}$ disconnects $T$. More precisely, the graph $(V, E_T - \{ (x,y)\})$ consists of precisely two disjoint connected components, one containing $u$, say $T_u$, and the other one containing $v$, say $T_v$. Since both $T_u$ and $T_v$ are in fact subgraphs of $T$ which is a tree, both of them are actually subtrees of $T$. Now consider an edge $(u,v)$. Since $(u,v)$ is a minimum weight edge crossing the cut and since $(x,y)$ is crossing the cut, we have $w((u,v)) \leq w((x,y))$. Clearly, since $(x, y)$ is crossing the cut, $(x,y) \not \in A$. Also, since $(u,v)$ is connecting two disjoint connected components, the addition of $(u,v)$ to $E_T - \{ (x,y)\}$ cannot induce a cycle and must connect $T_u$ and $T_v$. The resulting graph $T'$ is therefore a tree since it is connected and has no cycles. Moreover, since $T$ was spanning, so is $T'$ since it is connected and has the same vertex set as $T$. We deduce $T'$ is also a spanning tree of $G$.
Now, we examine the weight of the spanning tree $T'$:

Since $T$ was a minimum spanning tree $w(T) \leq w(T')$. By combining two above results we obtain $w(T) = w(T')$. Hence $T'=(V, (E_T - \{ (x,y)\}) \cup \{ (u,v) \})$ is a minimum spanning tree containing $(u,v)$. Since $A \subseteq E_T$ and $(x,y) \not \in A$, we have that the set
$(A \cup \{(u,v)\}) \in T'$, as desired. This completes the proof. $\blacksquare$

Prim’s Algorithm

Intuitive Minimum Spanning Tree Algorithm

Now, using the Theorem 6, we can think of an algorithm which gradually builds a minimum spanning tree. We start from some vertex $v \in V$ and consider the cut $(\{v\}, V - \{v\})$. Since $A=\emptyset$ must be present as a subset of any minimum spanning tree edge set, by selecting the least cost edge from $v$, say $(v,w), w \in V$ we can safely consider $\{(v,w)\}$ as a subset of some minimum spanning tree which is justified by Theorem 6. We repeat the process until we do not obtain a minimum spanning tree. We have just described the hand-wavy Prim’s algorithm. A careful reader may question the convergence of the process discussed and that will be addressed in the proof of the correctness of Prim’s algorithm.

Prim’s Algorithm implementation

Assumptions

Assume that the variable $Q$ holds the instance of a priority queue abstract data type. In the context of this algorithm, we assume that the priority queue is implemented as a binary heap.

Theorem 7: Proof of Correctness of Prim’s algorithm

Claim: Procedure Prim correctly computes the cost and the edge set of some minimum spanning tree.

Proof: (By induction)

We will consider the following invariant and prove it by induction:

Prior to the $i$-th iteration of the while loop, where $1 \leq i \leq |V|$, the set $S$ contains the vertices of the ‘partial’ minimum spanning tree defining the cut $(S, V-S)$, the set $A$ contains the edges of the ‘partial’ minimum spanning tree which are subset of edges of some actual minimum spanning tree and no edge in the set $A$ crosses the cut $(S, V-S)$. The priority queue $Q$ stores vertices in $V-S$ whose key is the cost of the minimum cost edge crossing the cut entering each vertex.

Basis: Prior to the first iteration of the while loop, corresponding to $i=1$, $A=\emptyset$, $S=\emptyset$. Trivially, $(\emptyset, V)$ is a cut while $A$ is a subset of the edge set of any minimum spanning tree. The for loop in the line 2 ensures $Q$ is initialised correctly. Since there are no edges crossing the graph cut $(S, V-S)$ the initialisation of $Q$ is indeed correct, so the basis is established.
Induction Assumption: Assume that the stated invariant holds for all iterations upto the $i$-th iteration of the while loop.
Induction Step: By the invariant, the set $S$ contains the vertices of the ‘partial’ minimum spanning tree defining the cut $(S, V-S)$ and the set $A$ contains the edges of the ‘partial’ minimum spanning tree which are subset of edges of some actual minimum spanning tree and no edge in the set $A$ crosses the cut $(S, V-S)$. In the while loop body, the vertex $u$ is extracted from the priority queue.
The cut $(S, V-S)$ is updated to $(S \cup \{ u\}, V - (S \cup \{ u\}))$.
Suppose $u=s$. Then $u$ is the start vertex and there was no incoming edge. Observe that since $u$ is the start vertex, the graph $(S, \emptyset)$ is a tree and since $A$ is empty, it remains the subset of some minimum spanning tree while it does not cross the cut $(S, V-S)$. We conclude that the graph $(S \cup \{ u\}, \emptyset)$ is a tree.
Suppose $u \neq s$. By the invariant, $(u.parent, u)$ is the minimum cost edge crossing the cut $(S, V-S)$ entering the vertex $u$. By Theorem 6, $A \cup \{(u.parent, u)\}$ is a subset of edges of some minimum spanning tree. Lines 14,15 correctly update the set $A$ to $A \cup (u.parent, u)$ and correctly increment the cost of the ‘partial’ minimum spanning tree built so far. Since $(S, A)$ was a tree and $(u.parent, u)$ is a crossing edge, $A \cup (u.parent, u)$ does not induce any cycle so the graph $(S \cup \{ u\}, A \cup \{(u.parent, u)\})$ remains a tree.
Now the for loop in the line 16 considers all possible outgoing edges of $u$. Observe that all those edges $(u,v)$, where $v$ is a vertex adjacent to $u$ are actually crossing edges. The conditional in line 17 correctly updates values of the minimum cost edge entering any vertex in the set $(V-S) - \{ u \}$ if the update is necessary. Observe that those updates maintain the statement regarding $Q$ in the invariant. It is possible that not all crossing edges affecting $Q$ are considered. This is fine since the invariant for $i$-th iteration guarantees that crossing edges which are not updated are still the least cost crossing edges. Therefore, the invariant is established for the next iteration.

Now consider what happens at the termination of the while loop. The while loop terminates precisely when $Q=\emptyset$. But then $S=V$. By the invariant proved before, the ‘partial’ minimum spanning tree includes all vertices in $V$. By the invariant, $A$ is the set of edges of the ‘partial’ minimum spanning tree which is also subset of edges of some minimum spanning tree. By invariant, $(S,A)$ is a tree. Since $S=V$, we deduce $(S,A)$ is a spanning tree. Since $A$ is the subset of edges of some minimum spanning tree, we deduce $(S,A)$ is a minimum spanning tree. By invariant, the cost $\kappa$ of $(S,A)$ was computed correctly. This completes the proof. $\blacksquare$

Some observations

• According to Theorem 4, there exists a minimum spanning tree containing the least cost edge. Observe that this will be the top edge in the priority queue, which will be the first edge used to connect source vertex $s$ in the Prim’s algorithm
• It is possible to adapt Prim’s algorithm to count minimum spanning trees. Observe that Prim’s algorithm implicitely resolves ties with respect to the edge cost by taking the first discovered edge of the particular cost. By performing the process of considering all edges of particular cost in growing a ‘partial’ minimum spanning tree, by using any complete graph search algorithm (BFS, DFS, …) we can enumerate all minimum spanning trees.

Running time analysis of Prim’s Algorithm

Claim: Procedure Prim executes $O((|E|) \cdot log(|V|))$ operations.

Proof: Let $T_{Prim}(|E|, |V|)$ be the number of operations executed in the procedure Prim.

• The for loop in the line 2 executes precisely $|V|$ times and its body performs only constant time operations. Hence, there are $\theta(|V|)$ operations performed in this loop
• Line 5 is a constant time operation
• Line 6 is a min heap heapify operation which takes $O(|V|)$ operations
• Lines 7 to 9 are constant time operations

Now we analyse the main while loop. Each vertex gets extracted once and only once from the heap $Q$. Each extraction operation takes $O(log|V|)$ operations. Observe that once that regardless of whether or not the if in the line 13 passes, there are at most constant number of operations in the while loop body except the inner for loop. Observe that for loop executes once and only once for each edge in $E$ across the whole execution of the algorithm. There are $O(log |V|)$ operations spent in each heap update. Since each edge gets considered from both endpoints, there can be at most $2 \cdot O(|E|) = O(|E|)$ heap operations throughout the whole execution of the algorithm coming from processing edges. Each such operation itself causes rebalancing the heap and hence takes $O(log |V|)$ operations. Hence the inner for loop contributes with $O(|E| log |V|)$ operations throughout the whole execution of the algorithm. Recall, since the graph $G$ is connected, $|E| \geq |V| - 1$.

By summing up all contributions, we get:

This completes the analysis. $\blacksquare$

Kruskal’s Algorithm

Unlike Prim’s algorithm, which constructs a minimum spanning tree by ‘growing’ a single ‘partial’ minimum spanning tree, Kruskal’s algorithm takes a different approach. Kruskal’s algorithm relies on cleverly merging subtrees of a ‘forest’ until the ‘forest’ becomes a tree. Main idea is to start from a forest of $|V|$ leaves representing each vertex and in each step connect two disjoint forest components corresponding to the least cost ‘crossing’ edge. Theorem 6 gives conditions which guarantee the components merged in the process remain subtrees of some minimum spanning tree.

Here is a bit deeper explanation. Clearly, every vertex must be included in some minimum spanning tree. Hence every component in the initial forest of singleton vertex trees is a part of some minimum spanning tree. We can think of this as a ‘base’ case. Now, suppose that we have a forest of components (trees) $\{ C_1, C_2, \ldots, C_k\}, 1 \leq k \leq |V|$ for some $k$. Assume all $\{ C_1, C_2, \ldots, C_k\}$ are parts of some (not necessarily the same) minimum spanning tree. Suppose $A$ is the set of edges of the forest. Now let $(u,v)$ be the edge connecting two distinct components, $C_i, C_j, 1 \leq i, j \leq k$ where $i \neq j$ and $u \in C_i, v \in C_j$. Observe that $(u,v)$ is crossing the cut $(C_i, V - C_i)$. By Theorem 6, $A \cup \{ (u,v) \}$ is a subset of some minimum spanning tree. Observe that the number of components decreases by one every time a merge is performed. Hence the process completes after exactly $|V|-1$ iterations. One challenge is quickly determining whether $u$ and $v$ belong to distinct components. It turns out there is a data structure solving exactly this problem - disjoint sets. This process is the main intuition behind Kruskal’s algorithm:

Theorem 8: Proof of Correctness of Prim’s algorithm

Claim: Procedure Kruskal correctly computes the cost and the edge set of some minimum spanning tree.

Proof: (By induction)

We will consider the following invariant and prove it by induction:

Prior to the $i$-th considered edge in the for loop in line 10, where $1 \leq i \leq |E|$, the set $A$ contains the edges of the forest $\{ C_1, C_2, \ldots, C_k\}, 1 \leq k \leq |V|$. $A$ is a subset of edges of some minimum spanning tree. Furthermore, $A$ contains all and only the edges which were minimum cost crossing edges connecting disjoint components discoverable in the first $i - 1$ edges of $E$ in the sorted order. Edges in $A$ are the first discovered such edges.

Basis: Consider $i=1$. By the for loop in the line 5, there are precisely $|V|$ disjoint singleton trees in the forest $\{ C_1, C_2, \ldots, C_k\}, k = |V|$. Since the edge set $A$ is $\emptyset$, and $\emptyset$ is a subset of any minimum spanning tree edge set, the invariant holds.
Induction Assumption: Assume the claim holds for $i-1, i \geq 1$.
Induction Step: Consider $i$-th iteration. Suppose $u \in C_i, v \in C_j, 1 \leq i,j, \leq k$. Firstly, we prove that $e=(u,v)$ causes the union operation $\iff$ $e$ is a minimum cost edge crossing the cut $(C_i, V-C_i)$ where no edge in $A$ crosses $(C_i, V-C_i)$.
$(\leftarrow)$ Suppose $e=(u,v)$ causes the union operation. Then the correctness of disjoint set $\texttt{FindSet}$ means $i \neq j$ so $u$ and $v$ belong to disjoint components $C_i$ and $C_j$. Now consider the cut $(C_i, V-C_i)$. Since $A$ contains all and only the edges in current forest and $i \neq j$, it must be the case $u$ and $v$ are not connected in the current forest. But then, $A$ contains no edge crossing the cut $(C_i, V-C_i)$ because otherwise $u$ and $v$ would be connected. We claim that $(u,v)$ is the minimum cost edge to connect $u$ and $v$ directly or indirectly. By the sorted order of $E$, if there existed an edge to connect connect $u$ and $v$ directly or indirectly, that edge had to have the strictly smaller cost than $(u,v)$ and had to appear before $(u,v)$. But then, by invariant, that edge had to cause the union operation in some previous iteration. This means that $(u,v)$ now belong to the same connected component. This contradicts the fact $i \neq j$. Hence $(u,v)$ is indeed a minimum cost edge to connect $u$ and $v$ directly or indirectly.
$(\rightarrow)$ Suppose $e$ is an edge crossing the cut $(C_i, V-C_i)$ where no edge in $A$ crosses $(C_i, V-C_i)$. Then, by the correctness of disjoint set $\texttt{FindSet}$, $\texttt{FindSet(u)} \neq \texttt{FindSet(v)}$ so the union occurs.

We condition on whether $e=(u,v)$ causes the union operation or it does not.
Suppose $e=(u,v)$ causes the union operation. By the proof of the previous claim, $e=(u,v)$ is a minimum cost edge crossing the cut $(C_i, V-C_i)$ where no edge in $A$ crosses $(C_i, V-C_i)$. Since $A$ is a subset of edges of some minimum spanning tree, by Theorem 6, $A \cup \{(u,v)\}$ is also a subset of edges of some minimum spanning tree. The algorithm correctly updates $A$ and $\kappa$ in lines 13,14 while correctly merges $C_i$ and $C_j$ in line 12. This establishes the invariant for the next iteration.
Suppose $e=(u,v)$ does not cause the union operation. Then $\texttt{FindSet(u)} = \texttt{FindSet(v)}$. Then $u$ and $v$ belong to the same component, so $A$ contains some edge crossing $(C_i, V-C_i)$. By the invariant, that edge had smaller or equal cost then $(u,v)$ so $(u,v)$ cannot improve the current forest and can only induce a cycle. Hence $A$ must not contain $(u,v)$. Components remain untouched so the invariant for the next iteration holds by the previous invariant and the fact $(u,v)$ should not be included in the set $A$.
This proves the induction step.

After the termination of the main for loop, $A$ is a subset of edges of some minimum spanning tree. We claim $(V, A)$ is a minimum spanning tree. There are precisely $|V| - 1$ edges in any minimum spanning tree and all of them are connecting some disjoint components since removal of each edge disconnects that minimum spanning tree. Furthermore, all those edges are the minimum cost edges crossing some cut, because otherwise we can contradict the optimality of the minimum spanning tree by replacing them with a better alternative. We will show $A$ contains $|V| - 1$ edges. Assume $(u,v)$ is a minimum cost edge crossing some cut $(C_i, V-C_i)$. By the invariant, if $(u,v)$ is the first such an edge in the sorted order of $|E|$ it will be included in $A$. Otherwise, there existed some other edge $(u', v')$ crossing the same cut $(C_i, V-C_i)$ which was discoverable before $(u,v)$ which was included in $A$ by the invariant. Since $(u,v)$ was arbitrary, $|A| = |V| - 1$. Now, since any minimum spanning tree contains precisely $|V| - 1$ edges and $A$ is a subset of edges of some minimum spanning tree with $|A| = |V| - 1$, we deduce $(V,A)$ is a minimum spanning tree. This implies the correctness of the Kruskal’s algorithm. $\blacksquare$

Some observations

• According to Theorem 4, there exists a minimum spanning tree containing the least cost edge. Observe that this will be the first edge in sorted edge set, which will be the first edge used to connect two leaves in the Kruskal’s algorithm.
• An efficient implementation of Kruskal’s algorithm relies on disjoint sets data structure, which is a very specific and interesting data structure that can be implemented in many ways (as linked lists, as trees …). There are several obstacles in the implementation of disjoint sets which are solved by using path compression and weighted union heuristics.
• Kruskal’s algorithm relies on the fast implementation of some sorting algorithm, which is one of the fundamental problems in computer science. If the distribution of edge costs is known, a faster linear time sorting algorithm can be employed.
• Handling ties in Kruskal’s algorithm is very transparent and its execution is entirely deterministic after the sorting completes. Different sorting sorting algorithms used to sort edges may result in different resulting minimum spanning trees.

Running time analysis

Claim: Procedure Kruskal executes $O(|E| \cdot log(|E|))$ operations.

Proof: Let $T_{Kruskal}(|E|, |V|)$ be the number of operations executed in the procedure Kruskal. Now:

• Lines 2..4 are constant time operations
• The for loop in the line 5 contributes to $|V|$ disjoint set make operations
• The for loop in the line 7 executes $|E|$ times and its body is a constant time operation.
• Assuming the usage of the optimal comparison based sorting algorithm, the operation in line 9 takes $O(|E|log(|E|))$ operations.

Now we apply the aggregate analysis to the main for loop in the line 10. Clearly, the main for loop executes precisely $|E|$ times and each $\texttt{FindSet}$ operation takes constant number of operations (by the properties of disjoint set data structure). Hence each execution of the main for loop takes at least $2 \cdot O(1) = O(1)$ number of operations. Now we will count the number of executions of the if body throughout entire execution of the main for loop. By Correctness of Kruskal’s algorithm, there will be exactly $|V|-1$ edges in $A$. But that means there are exactly $|V|-1$ disjoint set union operations corresponding to executions of if body throughout entire execution of the main for loop. Using the properties of disjoint set data structure with weighted union, throughout entire execution of the algorithm, all disjoint set operations take $O(|V| + |V|-1 + |E| + |V|log(|V|)) = O(|V|log(|V|)$ atomic operations. Assuming the graph is connected, we have $|E| \geq |V| - 1$ so $|V| = O(|E|)$.