Writing a console calculator using Haskell

Recently, I have been exploring the interesting world of compiling techniques and formal languages. During the last two months, I have encountered many classes of formal language grammars and I have decided to dedicate a bit of time to one of the classical examples of context-free grammars - arithmetic expression grammar.

I wanted to practice writing hand-coded lexers and parsers while learning about compilers. This seemed like a perfect occasion to brush up Haskell ‘skills’ I have acquired in the functional programming course I have taken recently at University. Also, I wanted to make something ‘practical’ and something I can easily show - a simple console calculator.

In this post, I am going to discuss several interesting phases of solving the ‘easy’ problem of correctly evaluating basic arithmetic expressions. We are going to touch a few formal languages, a bit of Haskell and a bit of software engineering practice to ensure our calculator actually works :)

Here is a link to the project github repository.

Introduction

calc (1 + 2) * (5 - (4 / 2))
9.0

calc is a very simple console calculator. So far it supports the following expression types:

• Basic arithmetic +, -, *, / → like 1 + 2 * 3
• Parenthesised expressions → like (1 + 2) * 3 - ((2 - 1)/(4 + 2))
• Unary minus → like -(-(2+3))

Expressions can have an arbitrary number of whitespaces between characters and will be computed correctly as long as they are lexically and semantically valid. We are going to define the expression grammar very rigorously in one of the next sections.

The implementation consists of :

• Encoding arithmetic expressions as a stream of tokens (see Tokens.hs)
• Encoding arithmetic expressions as an abstract syntax tree (see Ast.hs)
• Lexical analysis (see Lexer.hs)
• Parsing a stream of tokens (see Parser.hs)
• Evaluation of a valid abstract syntax tree (see Evaluator.hs)

Unit tests are written using Hspec and cover:

• Lexical analysis (see LexerSpec.hs)
• Parsing (see ParserSpec.hs)
• Evaluation (see EvaluatorSpec.hs)

A brief algorithm description

To perform expression evaluation, calc performs these steps in order:

1. lexically analyses the input string - checks whether every character is a valid character and builds a stream of tokens
2. parses the stream of tokens produced by the previous step - builds the expression syntax tree taking account for operator precedence, nested expressions …
3. evaluates the expression tree produced from the previous step

Everything is put together here.

You can see how it works in the interactive mode here:

Implementation

Lexical analysis

Now, a bit of formal language theory reminds us that the lexical structure of arithmetic expressions is a regular language. This implies that there exists a DFA that recognises that language. In terms of a practical application, we can construct a regular expression for each lexical category of arithmetic expression language and build a minimal DFA to recognise it.

Before we go deeper into the inner workings of lexical analyser, we introduce the following lexical categories - tokens:

• Operator which is a single character
• Number which is a double
• OpenParens ’(’ and CloseParens ’)’

Haskell algebraic data types are a very powerful tool to model this structure simply as:

data Token =  Operator Char | 
              Number Double |  
              OpenParens    | 
              CloseParens 
              deriving (Show, Eq)

Now after we have neatly defined tokens structure we need to think about how we want to recognise them. The heart of any lexical analysis task is to take a raw input string and produce a stream of tokens. In this case, we simplify the situation by returning a list of tokens instead of the ‘proper’ buffered stream.

There are many tools to construct the lexer automaton from regular expressions for tokens. But in this case, with a bit of pen and paperwork, it was possible to design a simple automaton to recognise tokens.

Said in simple words, the automaton goes character by character and it tries to match the longest possible token. It maintains the stack of successfully matched states up to the current character and performs state transition on each consumed character. When the automaton ends up in the accepting state, that state is pushed on the ‘history’ stack. This strategy is known as maximal munch tokenisation.

The automaton has the following states:

data LexerState = Start          |
                  Digits         |
                  DigitsAfterDot |
                  Operators      |
                  Parens         |
                  Error
                  deriving (Show)

Haskell’ s powerful pattern matching makes it very easy to implement this logic. In the code snippet below, you can see all state transitions and history maintenance when the automaton is in the ‘Digits’ state. To complete the automaton, we write such expressions for every possible state and transition.

consume [] Digits history tokens = consume [] Start [] ((Number number):tokens)
  where number = read (historyAsStr history) :: Double
consume input@(x:xs) Digits history tokens
  | isDigit x = consume xs Digits ((Digits, x) : history) tokens
  | isSpace x = consume xs Digits history tokens
  | x == '.'  = consume xs DigitsAfterDot ((Digits, x) : history) tokens
  | otherwise = consume input Start [] ((Number number):tokens)
  where number = read (historyAsStr history) :: Double

Finally, our lexical analysis becomes simply a method lexicallyAnalyse :: String -> Maybe [Token]. Maybe type is here to indicate that we either correctly lexically analyse or the input string does not match our language.

lexicallyAnalyse :: String -> Maybe [Token]
lexicallyAnalyse input = consume input Start [] []

You can see the full implementation here.

Optimising the grammar

Before we start thinking about parsing expression grammar, we need to ensure we have correctly defined the grammar and that our grammar is ‘optimal’ from the perspective of a hand-coded parser.

To make the algorithm description more accurate, we are going to use a bit of a formalism. The grammar used to implement calc will be the following one:

Exp   -> Term Exp'
Exp'  -> + Term Exp'
      |  - Term Exp'
      | ε
Term  -> Factor Term'
Term' -> * Factor Term'
      |  / Factor Term'
      | ε
Factor -> - Factor
      | Atom
Atom -> Number
      | ( Exp )

At first, this grammar seems to be an overkill and it feels overcomplicated for the ‘simple’ problem of doing elementary school arithmetic. One might ask, why did not we use productions like:

Exp   -> Exp + Exp
      |  Exp - Exp
      |  - Exp
      | (Exp)
      ...
      | Number

instead of the ones described the above? The second grammar is clearly more readable and conveys the ‘meaning’ more directly.

The only reason lies in the structure of the second grammar. After doing a bit of pen and paperwork, it is not hard to observe that the second grammar is ambiguous. How many distinct parse trees are for the expression 1 + 2 + 3 ? Apart from being ambiguous, this grammar is left recursive since the Exp nonterminal appears to the right side of the definition of Exp. These two properties are not very desirable since they complicate parsing. In fact, the only fact that the grammar is left recursive rules out recursive descent parsing - one of the most famous parsing algorithms. The reason is easy to see. A recursive descent algorithm could end up in an infinite recursion by always expanding the leftmost terminal without consuming any input. This property implies stack overflow and immediately rules out top-down techniques.

However, this grammar happens to have an equivalent, unambiguous, right-recursive ‘cousin’. This ‘cousin’ is actually the first grammar presented. How one could obtain the ‘proper’ grammar? To remove ambiguity, we simply introduce more nonterminal symbols. The intuition is that we want some operators to bind more ‘tightly’ which reflects their ‘precedence’. We want a + b * c to be parsed as a + (b * c). So we introduce nonterminals Exp, Factor and Atom which are still left recursive, but the new grammar is not ambigous. It suffices to eliminate the left recursion from all productions. There is a systematic process that often works :

1. Perform left factoring of common parts of each production
2. Eliminate left recursion using a set of rewrite rules

Although it can be (partially) automated, in the case of this grammar a bit of pen and paperwork was sufficient.

The final result is the first grammar and the complete process is explained clearly here.

Parsing

The expression tree which we are going to use is a direct implementation of the above-described grammar and is implemented using algebraic data types:

data Exp    = NontrivialExp { expTerm :: Term, expExp' :: Exp' }
            | TrivialExp
            deriving (Show, Eq)
data Exp'   = NontrivialExp' { exp'Op :: ArithOp, exp'Term :: Term, exp'Exp' :: Exp'}
            | TrivialExp'
            deriving (Show, Eq)
data Term   = NontrivialTerm { termFactor :: Factor, termTerm' :: Term' } deriving (Show, Eq)
data Term'  = NontrivialTerm' { term'Op :: ArithOp, term'Factor :: Factor, term'Term' :: Term' }
            | TrivalTerm'
            deriving (Show, Eq)
data Factor = NegativeFactor { innerFactor :: Factor }
            | AtomicFactor { innerAtom :: Atom }
            deriving (Show, Eq)
data Atom   = NumericAtom { number :: Double }
            | ExpAtom { innerExp :: Exp }
            deriving (Show, Eq)

data ArithOp = Add | Sub | Mul | Div deriving (Show, Eq)

The parsing algorithm is a form of backtrack-free, lookahead (1) recursive descent. The algorithm relies on the fact that the grammar used:

Exp   -> Term Exp'
Exp'  -> + Term Exp'
      |  - Term Exp'
      | ε
Term  -> Factor Term'
Term' -> * Factor Term'
      |  / Factor Term'
      | ε
Factor -> - Factor
      | Atom
Atom -> Number
      | ( Exp )

is LL(1) and hence can be parsed using the following LL(1) table:

As a consequence, we can parse it using mutually recursive expressions such as :

parseExp :: [Token] -> (Maybe Exp, [Token])
parseExp [] = (Just TrivialExp,[])
parseExp tokens@(lookahead : rest)
  | (Operator op)       <- lookahead  = parse' op
  | (Tokens.Number num) <- lookahead  = parse' 'n'
  | OpenParens          <- lookahead  = parse' '('
  | otherwise                         = (Nothing, tokens)
  where parse' look | look == '+' = (liftIntoExp term exp', resultRest)
                    | look == '-' = (liftIntoExp term exp', resultRest)
                    | look == '(' = (liftIntoExp term exp', resultRest)
                    | look == 'n' = (liftIntoExp term exp', resultRest)
                    | otherwise   = (Nothing, tokens)
                    where (term, termRest)   = parseTerm tokens
                          (exp', resultRest) = parseExp' termRest

Again, it is very easy to observe the power of Haskell’s type system and pattern matching against possible state and lookahead pairs. Thanks to the strength of Haskell’s type system and a great compiler, it was relatively easy to ensure that all parsing cases are covered. You can see the full implementation here.

Evaluation

Evaluation is performed using a simple inorder tree walk which is implemented as a set of mutually recursive expressions which destruct abstract syntax tree. An example of such expression is here:

evaluateExp' :: Exp' -> Double
evaluateExp' TrivialExp' = 0
evaluateExp' NontrivialExp' {
  exp'Op = op,
  exp'Term = term,
  exp'Exp' = rest
}
  | op == Add = evaluateTerm term + evaluateExp' rest
  | op == Sub = - evaluateTerm term + evaluateExp' rest

You can see the full implementation here.

Testing

Now once we have completed the implementation, we need to ensure it actually works. Using a typical Haskell Stack project, it was relatively easy to set up unit testing using HSpec. Although it is very popular in Haskell world to use monadic testing libraries such as QuickCheck which automatically generate inputs, I have decided to keep it simple and use a set of hand-crafted examples with expected outputs.

Since the implementation consists of three distinct parts (lexer, parser, evaluator) it was sensible to define test cases for those parts separately.

For example, one of test cases for the evaluator phase are:

tests :: Map Int (Exp, Double)
tests = fromList [
  (1, ((parsed . lexed) "1", 1.0)),
  (2, ((parsed . lexed) "- 1", -1.0)),
  (3, ((parsed . lexed) "- - ( 2 + 3 )", 5.0)),
  (4, ((parsed . lexed) "1.0 + 2.0 * 3.0 / ( 6.0*6.0 + 5.0*44.0)", 1.0234375)),
  (5, ((parsed . lexed) "1 + 2 * 3 ", 7.0)),
  (6, ((parsed . lexed) "1 * 2 + 3", 5.0)),
  (7, ((parsed . lexed) "-4 * (2 + 3)", -20.0)),
  (8, ((parsed . lexed) "1 + 2 + 3 + 4 + 5 + 6 + 7 ", 28.0)),
  (9, ((parsed . lexed) "1 +2 -3 +4 -5 +6 + 7 +8 + 9-10+  11", 30.0)),
  (10, ((parsed . lexed) "1 -2 + 4 - 2 *5 +3 * 6 *7+4 - 134 *5 ", -547.0)),
  (11, ((parsed . lexed) " ( 1 + 2) * (2 + 3) + (4 * 5) + (6 * 7) / ((5 -2) * (2 +4))", 37.33333333333333)),

Now the HSpec specification is simply:

module EvaluatorSpec (
  evaluatorSpec
) 

evaluatorSpec :: Spec
evaluatorSpec = do
  describe "evaluator tests ..." $ do
    it "correctly evaluates #1" $ do
      evaluate (fst (tests ! 1)) `shouldBe` (snd (tests ! 1))
    it "correctly evaluates #2" $ do
      evaluate (fst (tests ! 2)) `shouldBe` (snd (tests ! 2))
    it "correctly evaluates #3" $ do
        evaluate (fst (tests ! 3)) `shouldBe` (snd (tests ! 3))
    it "correctly evaluates #4" $ do
      evaluate (fst (tests ! 4)) `shouldBe` (snd (tests ! 4))
    it "correctly evaluates #5" $ do
      evaluate (fst (tests ! 5)) `shouldBe` (snd (tests ! 5))
    it "correctly evaluates #6" $ do
      evaluate (fst (tests ! 6)) `shouldBe` (snd (tests ! 6))
    it "correctly evaluates #7" $ do
      evaluate (fst (tests ! 7)) `shouldBe` (snd (tests ! 7))
      ...

Now when executing stack test we get something like:

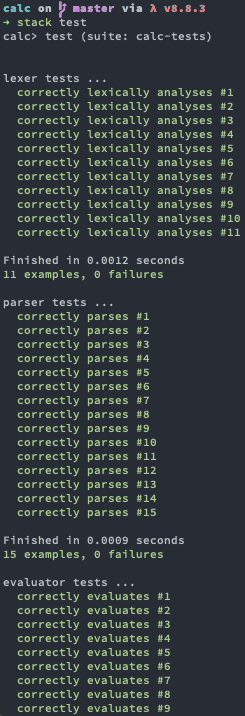
This unit testing setup made it possible to ensure that every refactor of each phase did not introduce a bug and it was very easy to detect some bugs related to operator precedence in expression evaluation.

To sum up all, it was very nice to see how functional programming comes into play with formal languages and I think I will continue to use Haskell for such tasks. It is just amazing to see how a type system of a programming language can directly implement both grammar and semantics for another ‘programming’ language. Moreover, the whole development experience using ghci interactive mode made it possible to isolate some small parts from the rest of the program and ensure they work while implementing them.